Strutt Help

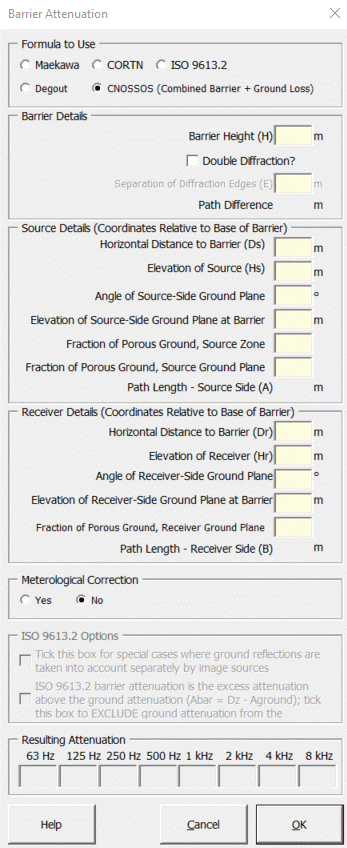
Strutt|Environmental Noise|Barrier Attenuation provides a barrier attenuation calculation, using either the Maekawa, ISO9613-2(1996), ISO9613-2(2024), Degout, CNOSSOS or CORTN method, which is entered in the active row of the worksheet.

The calculation is valid for the shadow or illuminated zone of the barrier and is limited to a maximum attenuation of (-) 25 dB at any frequency.

The CNOSSOS method of Barrier + Ground attenuation is also available and is discussed in detail here.

The Maekawa equation is implemented within the shadow zone as:

`IL = -[5 + 20log_10(sqrt(2 pi N_F)/tanh(sqrt(2 pi N_F)))]`

where,
`N_F = 2(delta/lambda)` is the Fresnel number

`delta` is the path difference, m
`lambda` is the wavelength of sound, m

The CORTN method gives a single-number dB(A) value, which is placed in Column E of the active row. In the Barrier Attenuation user form, the attenuation is displayed in the octave band cells, but the final result is a broadband value only, and selecting the CORTN method will NOT insert spectral values into the active row. The CORTN method is implemented using the following equation:

`IL = A_0 + A_1 x + A_2 x^2 + A_3 x^3 + ... + A_n x^n`

where,
`x = log(delta)` and `delta` is the path difference, m
The coefficients `A_n` are:

A0	A1	A2	A3	A4	A5	A6	A7
-15.4	-8.26	-2.787	-0.831	-0.198	0.1539	0.12248	0.02175

The ISO 9613-2 (1996) method includes an option to calculate the effect of meteorological conditions on the barrier attenuation, and is calculated as an insertion loss using:

`A_(b a r) = D_z - A_(g r) > 0`, over the top edge

`A_(b a r) = D_z > 0`, around a vertical edge

`D_(z) = -10log_10(3 + C_2/lambda C_3 delta K_(met))`

Where,
`A_(g r)` is the ground attenuation
`lambda` is the wavelength of sound at the frequency in question
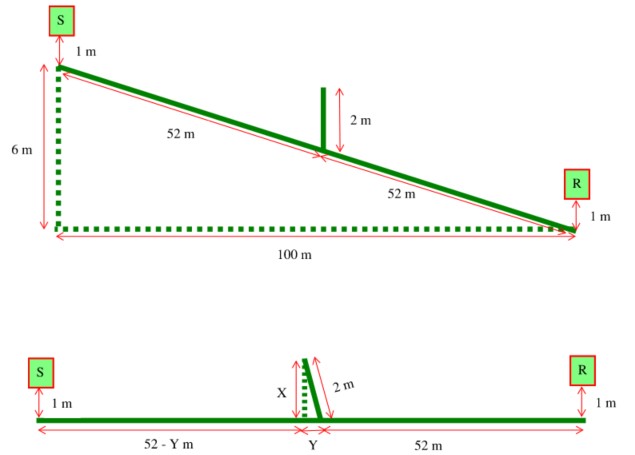
`delta` is the path difference between the diffracted sound and direct sound, calculated using: `delta = d_(ss) + d_(sr) + e - d`
`e` is the distance between the two diffraction edges in the case of double diffraction
`C_2 = 20` and includes the effect of ground reflections; if in sepcial cases ground reflections are taken into account separately by image sources, `C_2=40`
`C_3 = [1+((5*lambda)/e)^2]/[1/3+((5*lambda)/e)^2]` for double diffraction; `C_3 = 1` for single diffraction
`K_(met)` is a meteorological correction factor calculated using:

`K_(met) = exp(-1/2000 sqrt(d_(ss)d_(sr)d)/(2 delta))`, for `delta > 0`

`K_(met) = 1`, for `delta le 0`

`d_(ss)` is the distance from the source to the first diffraction edge, m
`d_(sr)` is the distance from the second diffraction edge to the reciever, m
`d` is the straight-line distance between source and receiver, m

• The barrier attenuation `D_(z)`, in any octave band, should not be taken to be greater than 20 dB in the case of single diffraction (i.e. thin barriers) and 25 dB in the case of double diffraction (i.e. thick barriers}.
• The ISO 9613.2 barrier attenuation is the excess attenuation above the ground attenuation. In some instances, it may not be appropriate to include ground attenuation in your calculation. For example, the ISO 9613.2 ground effect calculation is applicable only to ground which is approximately flat, either horizontally or with a constant slope. In addition, the ground effect component of the barrier calculation will break down should you attempt to use negative source or receiver heights. In some instances, you can use trigonometry to adjust the relative source and receiver heights to be positive, so that you can calculate the ground effect correctly. See image below as an example:

  

The ISO 9613-2 (2024) method is an updated methodology, with changes from the 1996 methodology as follows:

The Degout formula is calculated as follows:

`IL = {(0 " for " \ N_F < -0.25 ),(-6 + 12 sqrt(-N_F) \ " for " \ -0.25 <= N_F < 0 \ ),(-6 - 12 sqrt(N_F) \ " for " \ 0 <= N_F < 0.25 \ ),(-8 - 8 sqrt(N_F) \ " for " \ 0.25 <= N_F < 1.0 \ ),(-16 - 10log_10(N_F) \ " for " N_F > 1.0 \ ):}`