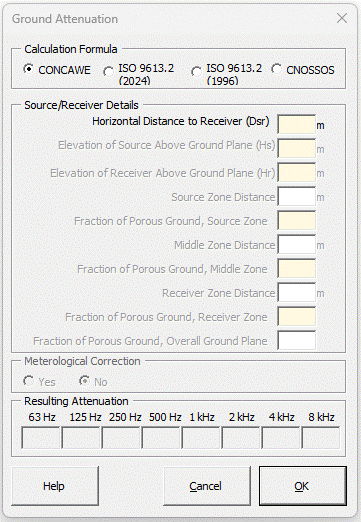
Strutt|Environmental Noise|Ground Attenuation inserts attenuation (dB) into the active row of the worksheet.
Input required is source and receiver heights, source to receiver distance and ground factors.
This method of calculating the ground effect is applicable only to ground which is approximately flat, either horizontally or with a constant slope.
Ground factors to be used are:
Hard ground: 0
Porous ground: 1
Mixed ground: 0 - 1
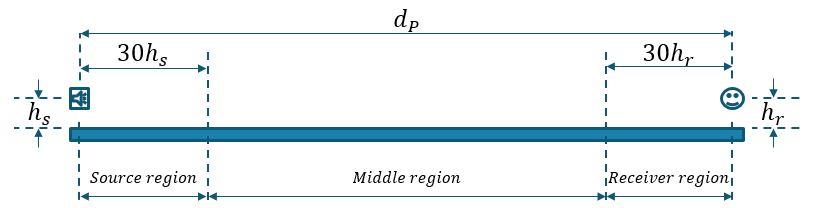
The ground effect is calculated by separating the distance between the source and receiver into 3 regions as:
The total ground attenuation for each octave band is calculated as:
`A_(gr) = A_s + A_r + A_m`
Where,
`A_s` is the source region attenuation
`A_r` is the receiver region attenuation
`A_m` is the middle region attenuation
`A_s`, `A_r` and `A_m` are calculated using:
| Nominal midband frequency, Hz | `A_s or A_r`*, dB | A_m, dB |
|---|---|---|
| 63 | `-1.5` | `-3q`** |
| 125 | `-1.5 + G xx a'(h)` | `-3q(1 - G_m)` |
| 250 | `-1.5 + G xx b'(h)` | |
| 500 | `-1.5 + G xx c'(h)` | |
| 1000 | `-1.5 + G xx d'(h)` | |
| 2000 | `-1.5(1 - G)` | |
| 4000 | `-1.5(1 - G)` | |
| 8000 | `-1.5(1 - G)` |
Notes:
`a'(h) = 1.5 + 3.0 xx e^(-0.12(h-5)^2)(1-e^(-d_P//50)) + 5.7 xx e^(-0.09h^2)(1 - e^(-2.8 xx 10^-6 xx d_P^2))`
`b'(h) = 1.5 + 8.6 xx e^(-0.09h^2)(1-e^(-d_P//50))`
`c'(h) = 1.5 + 14.0 xx e^(-0.46h^2)(1-e^(-d_P//50))`
`d'(h) = 1.5 + 5.0 xx e^(-0.9h^2)(1-e^(-d_P//50))`
-------------------------------
* For calculating `A_s`, take `G = G_s` and `h = h_s`. For calculating `A_r`, take `G = G_r` and `h = h_r`. See 7.3.1 (ISO 9613.2) for values of G for various ground surfaces.
** `{:(q = 0 , when \ d_P <= 30 (h_s + h_r)),(q = 1 - (30(h_s + h_r))/d_P, when \ d_P > 30(h_s + h_r) ):}`, where `d_P` is the source-to-receiver distance, in metres, projected onto the ground planes
Note this correction is only valid for source-receiver distances greater than 100 m.
Ground effects, `K_3`, are calculated as a function of distance for each octave band where:
63 Hz: `K_3 = 33.4 - 35.04log_10 d + 9.159(log_10 d)^2 - 0.3508(log_10 d)^3`
125 Hz: `K_3 = 8.96 - 35.8log_10 d + 20.4(log_10 d)^2 - 2.85(log_10 d)^3`
250 Hz: `K_3 = -64.2 + 48.6log_10 d - 9.53(log_10 d)^2 + 0.634(log_10 d)^3`
500 Hz: `K_3 = -74.9 + 82.23log_10 d - 26.921(log_10 d)^2 + 2.9258(log_10 d)^3`
1 kHz: `K_3 = -100.1 + 104.68log_10 d - 34.693(log_10 d)^2 + 3.8068(log_10 d)^3`
2 kHz: `K_3 = -7 + 3.5log_10 d`
4 kHz: `K_3 = -16.9 + 6.7log_10 d`
CNOSSOS is developed for propagation above varying-height ground planes, and uses the concept of equivalent height `z_s,z_r` - i.e. the source and receiver heights are defined relative to the average height of the ground plane, and are not necessarily the same as the local source/receiver heights `h_s,h_r`:
As well as the source-receiver geometry, the CNOSSOS model uses the ground factor `G` over the ground plane (i.e. proportion of porous ground). In cases where the ground plane consists of multiple ground types, the average `bar G` (weighted by the extent of each ground type) should be used.
Typical values of `G` are as follows:
The CNOSSOS model predicts the attenuation under neutral (or "homogenous") atmospheric conditions (constant sound speed where sound propagation paths are straight rays), as well as adverse (or "favourable") conditions where a sound speed gradient results in curved ray paths.
The effect of the curved ray paths is to increase the average propagation height and reduce the strength of the ground effect.
Under neutral conditions, the ground attenuation is calculated as:
`A_(ground) = -"Max" {(-10 log_10 (4 k^2/d_(SR)^2(z_s^2-sqrt((2 C_f)/k) z_s + C_f/k)*(z_r^2-sqrt((2 C_f)/k)z_r + C_f/k))),(-3(1-bar G_w)) :}`
where:
`k` is the wavenumber
`C_f=d_(SR) (1+3 w d_(SR) e^(-sqrt(w d_(SR))))/(1+w d_(SR))`
`w = 0.0185 (f^2.5 bar G_w^2.6)/(f^1.5 bar G_w^2.6 + 1.3*10^3 f^0.75 bar G_w^1.3 + 1.16*10^6)`
`bar G_w` is either the corrected ground factor `bar G prime` or the uncorrected ground factor `bar G`, depending on the calculation type:
(The CNOSSOS ground module is also used by the CNOSSOS diffraction module to calculate the ground reflection from the source to the diffraction edge `Delta_(ground(S,O))` and from the diffraction edge
to the receiver `Delta_(ground(O,R)`; the ground factor term is taken as either the modified or the unmodified term as outlined in the table below)
Under adverse conditions, the ground attenuation is calculated as:
`A_(ground) = -"Max" {(-10 log_10 (4 k^2/d_(SR)^2(hat z_s ^2-sqrt((2 C_f)/k) hat z_s + C_f/k)*(hat z_r^2-sqrt((2 C_f)/k) hat z_r + C_f/k))),(-3(1-bar G_m) \ " for " \ d_(SR)<=30(z_s+z_r)),(-3(1-bar G_m)*(1+2*(1-(30(z_s+z_r))/d_(SR))) " otherwise") :}`
where:
`hat z_s = z_s+ Delta z_s + Delta z_t` is the effective source height under adverse conditions
`hat z_r = z_r + Delta z_r + Delta z_t` is the effective receiver height under adverse conditions
`Delta z_s = a_0(z_s/(z_s+z_r))d_(SR)^2/2` is the change in effective source height due to the curvature of the sound paths
`Delta z_r = a_0(z_r/(z_s+z_r))d_(SR)^2/2` is the change in effective receiver height due to the curvature of the sound paths
`Delta z_t = 6*10^-3 d_(SR)/(z_s+z_r)` is the change in effective source/receiver height due to atmospheric turbulence
`a_0` is the inverse of the radius of curvature of the sound paths. A default value of `a_0 = 2*10^-4` is provided in CNOSSOS, however this could potentially be user-modified in Strutt if required.
`bar G_m` is either the corrected ground factor `bar G prime` or the uncorrected ground factor `bar G`, depending on the calculation type.
References: