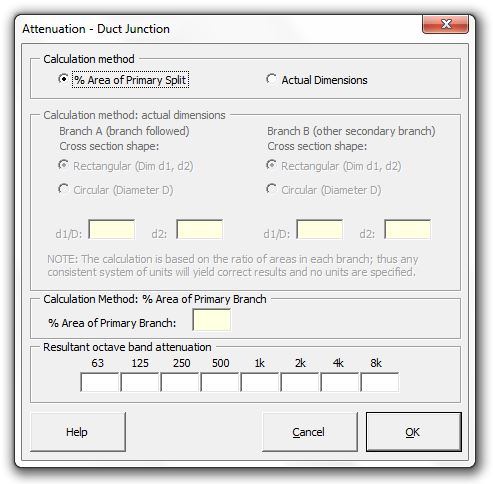

Strutt|Mechanical Services|Duct Elements|Split/Junction inserts octave band adjustments into the active row of the worksheet.

The attenuation of sound power at a junction that is related to the sound power transmitted down an individual branch of the junction is given by:
`Delta L_(Bi) = 10log_10[1-(((sum S_(Bi))/S_M - 1)/((sum S_(Bi))/S_M + 1))^2] + 10log_10(S_(Bi)/(sum S_(Bi)))`
where:
`S_(Bi)` is the cross-sectional areas of the individual branches
`S_M` is the cross-sectional area of the main feeder duct
The first term in the equation is related to the reflection of the incident wave when the area of the branches differs from the area of the main feeder duct. It is present only when the sound waves propagating in the main feeder duct are plane waves and when `sum S_(Bi) != S_M`.
Plane wave propagation in a duct exists at frequencies below:
`f_(c_0) = c_0/(2a)`
Where,
`c_0` is the speed of sound in air (ft/s)
`a` is the larger cross-sectional dimension (ft) of a rectangular duct
or:
`f_(c_0) = 0.586 c_0/d`
Where,
`d` is the diameter (ft) of a circular duct
`f_(c_0)`, the cutoff frequency, is the frequency above which plane waves no longer propagate in a duct.
If the total cross-sectional area of the branches after the junction is equal to the cross-sectional area of the main feeder duct, or if the frequencies of interest are above the cutoff frequency:
`Delta L_(Bi) = 10log_10(S_(Bi)/(sum S_(Bi)))`
References: