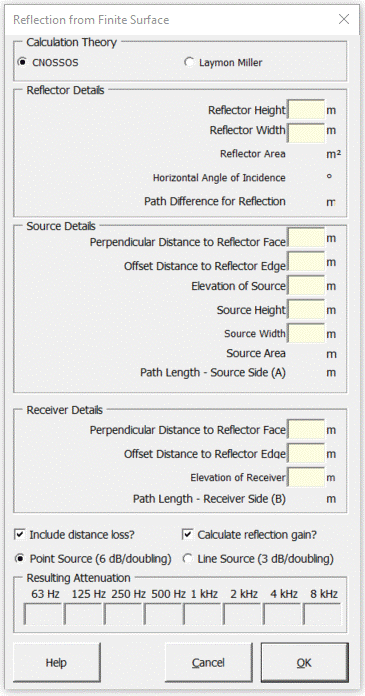

Strutt|Environmental Noise|Reflection from Surface inserts the reflection strength (in dB relative to the direct sound) for a finite-sized reflector into the active row of the worksheet.

The CNOSSOS reflection loss is termed "retrodiffraction" in the CNOSSOS paper, and accounts for the diffraction of some of the sound energy when a reflection occurs close to the edge of a finite-sized reflector - i.e. some of the energy is scattered by diffraction, which reduces the strength of the reflected sound.
The CNOSSOS model predicts the reflection strength `Delta L_w` of the image source. In the Strutt implementation of CNOSSOS, the distance loss for the reflected path (calculated using the Ratio of Distances calculation for either point or line source propagation) is by default added to `Delta L_w` to obtain the overall reflection strength relative to the direct sound. This simplifies the calculation by not requiring the user to conduct a completely new calculation using the image source as a new source.
Any significant absorption loss (i.e. `Delta L_alpha = 10 log_10(1-alpha)`) from the surface should be added manually by the user.
In theory, multiple reflections can be accommodated by successive application of the CNOSSOS reflection calculation to obtain the cumulative retrodiffraction loss.
The distance loss may be turned off, if needed, to simplify calculation of multiple reflections by 'stacking' successive CNOSSOS Reflection calculations.
However, for situations with multiple reflections (including semi-reverberant enclosures/courtyards) any image-source based method should be used with caution.
Consider using the Semi-Reverberant Courtyard calculation as an alternate.
The reflection loss is calculated using the path difference `delta` between the direct sound and the reflected path:
`delta = d_(SR)-d_(SO)-d_(OR)` - i.e. using a negative value of path difference.
`d_(SR)` is the source-receiver distance
`d_(SO)` is the distance from the source to the top of the reflector
`d_(OR)` is the distance from the top of the reflector to the receiver.
In effect, the reflection calc is treated as a 'flipped' barrier calculation where source and receiver are both on the same side of the barrier:
The 'true' reflection geometry (blue line) is geometrically equivalent to the 'barrier' geometry (orange line) in calculating the path difference for reflection (i.e. orange line minus yellow line).
Because of the negative sign of the path difference `delta` in the reflection calc, the closer the specular reflection point is to the top of the barrier, the stronger the diffraction loss.
The reflection loss due to diffraction is calculated using the same formula as 'pure' barrier diffraction in CNOSSOS Barrier Attenuation only using the negative path difference, as explained above.
`Delta_("diff") = {(10 C_H log_10 (3+40/lambda delta) " if " 40/lambda delta >= -2),(0 " otherwise") :}`
where:
`lambda` is the wavelength
`delta` is the path difference for reflection)
`C_H` is a coherence coefficient that reduces the strength of the reflection effect at low frequencies where the reflector size is small relative to wavelength.
`C_H="Min"((f h"))/250,1)`, where
`f` is the frequency
`h` is the reflector height
Calculates the reflection gain from a finite-surface based on the source-reflector geometry, the size of the source and the size of the reflector.
Depending on the geometry of the situation, the strength of an individual reflection will range from 0 dB to 3 dB
Note that this calculation only considers a single reflection path. If multiple reflection paths exist, either apply the calculation separately for each reflection or (if semi-reverberant conditions exist) use the Semi-Reverberant Courtyard calculation
References: