Strutt Help

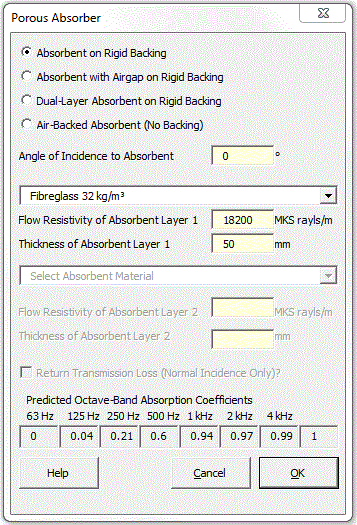
Strutt|Building Acoustics|Porous Absorber calculates the absorption coefficients or transmission loss of a porous absorber, and inserts the calculated values into the active row of the worksheet.

Strutt calculates absorption coefficients for the following absorber geometries:

• Porous absorber on rigid backing
• Porous absorber with airgap on rigid backing
• Dual-layer porous absorber on rigid backing
• Air-backed porous absorber (i.e. no backing)

Strutt calculates the absorption coefficients `alpha` from the complex pressure-reflection factor `R` between the surface of the absorber and the air using the following formula:

`R = (Z_S cos(phi)-Z_0)/(Z_S cos(phi)+Z_0)`

`alpha = 1-|R|^2`

where:
`Z_0` is the characteristic impedance (`rho C`) of air
`Z_S` is the surface impedance of the absorber
`phi` is the angle of incidence of the incident sound field

Strutt calculates the normal-incidence transmission loss using the complex pressure-transmission factor `T` of the construction and the power transmission coefficient `tau` using the following formulae:

`T = (2Z_S)/(Z_S+Z_0)`

`tau = |T|^2`

`"TL" = 10log_"10"(tau)`

The surface impedance of one layer of the absorber (`Z_(Si+1)`) is related to the surface impedance of the layer below it (`Z_(Si)`) using:

`Z_(Si+1) = (-j Z_(Si) Z_i cot(k_(x i) d_i) + Z_i^2)/(Z_(Si) - j Z_i cot(k_(x i) d_i))`

where:
`d_i` is the thickness of the layer
`Z_i` is the characteristic impedance of the layer
`k_(x i)` is the wavenumber for normal-incidence sound propagation in the layer

The surface impedance of the bottom layer of the absorber is found using the above formula, but imposing either:

• a boundary condition where the lower surface is rigid (and therefore has infinite impedance). In this case the formula reduces to:
  
  `Z_1 = -j Z_i cot(k_(x i) d_i)`
• a boundary condition where the absorber is backed by a semi-infinite airspace, in which case:
  
  `Z_(Si)=Z_0`

For air, `Z_i = Z_0` and `k_(x i) = k_0 = omega//c`

For porous absorbent, `Z_i` and `k_(x i)` are calculated using the Delaney and Bazley formulation:

`Z_i = rho_0 c_0 (1 + 0.0571X^(-0.754) - j 0.087X^(-0.732))`

`k_i = k_0 (1 + 0.0978X^(-0.7)-j0.189X^(-0.595))`

where `X` is a frequency-dependent parameter given by:

`X = (rho_0 f)/sigma`

`sigma` is the flow resistivity (MKS rayls/m) of the porous absorbent.

A drop-down menu is provided giving flow-resistivity values for several common absorbent materials, or else the user may enter in the flow resistivity manually.

For oblique-incidence, the underlying theory is the same, except the complex wavenumber `k_i` now includes both normal `k_(x i)` and lateral `k_(y i)` propagation components:

`Z_(Si+1) = (-j Z_(Si) Z_i k_i/k_(x i) cot(k_(x i) d_i) + Z_i^2)/(Z_(Si) - j Z_i k_i/k_(x i) cot(k_(x i) d_i))`

`k_(x i) = sqrt(k_i^2-k_(i+1)^2 sin(phi_(i+1)))`

For multi-layer absorbers, the incidence angle `phi_i` in each absorber will vary according to Snell's Law and the relative speed of sound (and hence impedance/wave number) in each layer

Reference: TJ Cox and P D'Antonio (2004) Acoustic Absorbers and Diffusers: Theory, Design and Application, pp141-150 Spon Press