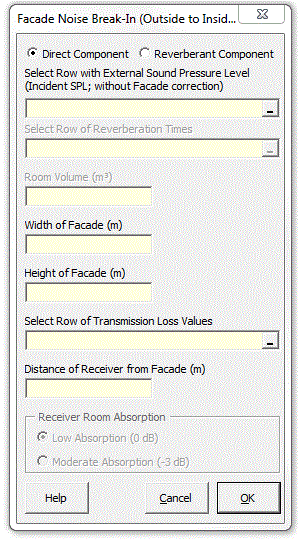

Strutt|Building Acoustics|Facade Noise Break-In calculates the noise break-in through a building facade and inputs it into the active row of the worksheet.

Strutt calculates either the direct or reverberant component of the noise break-in, toggled by an option button on the user form. The outdoor sound pressure level is the incident level at the facade (i.e. with NO facade correction)
The direct component is calculated by:
`L_(p,dir In) = L_(p,ext) + TL + 10log_10(S) + Delta L_("dist") + 10log_10(bar (cos beta))+10log_10(cos phi)`
where `Delta L_("dist")` is the distance correction for direct sound radiation from the facade, calculated using Distance Correction (Plane Source)
Strutt allows the user to (optionally) include angle of incidence corrections for the incident sound field, based on the approach of German Standards DIN 4109 and VDI 2713:
`beta` is the angle of view of the incident source (by default 0░ for a point source)
`phi` is the angle of elevation of the incident sound wave (by default 0░ for normal incidence)
The effect of the `10log_10(bar (cos beta))+10log_10(cos phi)` terms is to decrease the noise break-in to account for grazing incidence of sound onto the façade.
DIN 4109 uses default/typical values of 180░ for angle of view (`beta`) and 37░ for angle of elevation (`phi`), corresponding to an upper-floor receiver at a typical 7 m setback from the road edge.
For these values, `10log_10(bar (cos beta))= -2` and `10log_10(cos phi) = -1` resulting in an overall reduction of -3 dB relative to normal-incidence from a point source.
Note, however, that the reduction in the incident sound pressure at grazing incidence can be offset by a reduction in the transmission loss at high angles of incidence (e.g. at the coincidence frequency); for high angles of incidence the oblique-incidence transmission loss should be used where available. This will be eventually be able to be predicted with the Transmission Loss Prediction calculation.
Strutt provides two options for calculating the reverberant component
For low absorption in the receiving room `alpha_"ave" ~= 0.1`, traditional diffuse field theory gives:
`L_(p,rev In) = L_(p,ext) + TL + 10log_10(S) - 10log_10(A) + 6 + 10log_10(bar (cos beta))+10log_10(cos phi)`
For rooms with medium absorption `alpha_"ave"~=0.5`, BS8233 provides an alternate method:
`L_(p,rev In) = L_(p,ext) + TL + 10log_10(S) - 10log_10(A) + 3 + 10log_10(bar (cos beta))+10log_10(cos phi)`
where:
`TL` is the transmission loss of the partition (negative sign convention)
`S` is the total area of facade considered in the TL (m▓)
`A` is the area of absorption in the receiving room (m▓ sabin), back-calculated from the reverberation time (`RT`) and volume (`V`) of the room by `A = 0.161V//RT`